ニューラルネットワークが必要な背景

ロジスティック回帰によって非線形が可能になった。

ただ、膨大な数の説明変数(feature)が必要なものにロジスティック回帰を適用すると、ロジスティック回帰だと計算が追いつかなくなる。

膨大な数の説明変数(feature)の例としては、写真を見て「これが車であるか否かを判断する」する場合、$50 \times 50$ pixelのグレースケール画像でも、2,500変数で、2次式にしても約3,000,000個のパラメータを計算することになる。(RGBだとその3倍以上)。

そこで、よりよいアルゴリズムを有する人の脳にヒントを得たのがニューラルネットワーク(Neural Network)。

ニューラルネットワーク(Neural Networks)

下記は、入力X($x_1$, $x_2$, $x_3$)に対して、出力Y($h_\Theta(x)$)となる３層構造のニューラルネットワークの例である。

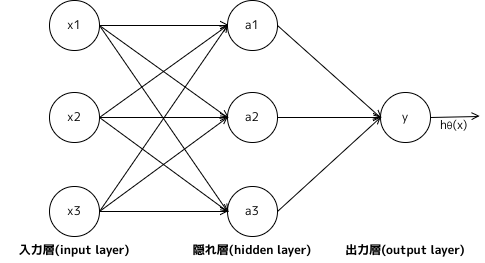
入力でもない、出力でもないレイアを隠れ層(hidden layer)といい、隠れ層(hidden layer)の各ノードをアクティベーションユニット(activation units)という。

$$ a_i^{(j)} = \text{レイア $j$ のアクティベーションユニット $i$} \\
\Theta^{(j)} = \text{レイア $j$ から レイア $j+1$ に移る際に使う重み行列} $$

上記の図のアクティベーションユニット(activation units)、及び出力は下記のように表現される。

$$ a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \\
a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \\
a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \\
h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) $$

ベクトル化した表現は下記のようになる。

$$ a^{(2)} = g(\Theta^{(1)}a^{(1)}) \\\
h_\Theta(x) = a^{(3)} = g(\Theta^{(2)}a^{(2)}) $$

つまり

$$ a^{(j)} = g(\Theta^{(j-1)}a^{(j-1)}) $$

レイヤ$j$からレイア$j+1$を計算する場合、下記のように表現できる。

$$ a^{(j+1)} = g(\Theta^{(j)}a^{(j)}) $$

これは、ロジスティック回帰と同じようなことを入力層から出力層に間で行っていることになる。

ニューラルネットワーク(Neural Networks)の例

AND

$$ \boldsymbol{ \Theta } = \begin{bmatrix} -30 & 20 & 20 \end{bmatrix} \\
\boldsymbol{ X } = \begin{bmatrix} 1 \\\ x_1 \\\ x_2 \end{bmatrix} \\
$$

$$ h_{ \Theta }(x) = g(\boldsymbol{ \Theta }\boldsymbol{ X }) = g(-30 + 20x_1 + 20x_2) $$

$$ \begin{array}{c|c|c} x_1 & x_2 & h_\Theta(x) \\
\hline 0 & 0 & 0 \\
1 & 0 & 0 \\
0 & 1 & 0 \\
1 & 1 & 1 \\
\end{array} $$

OR

$$ \boldsymbol{ \Theta } = \begin{bmatrix} -10 & 20 & 20 \end{bmatrix} \\
\boldsymbol{ X } = \begin{bmatrix} 1 \\\ x_1 \\\ x_2 \end{bmatrix} \\
$$

$$ h_{ \Theta }(x) = g(\boldsymbol{ \Theta }\boldsymbol{ X }) = g(-10 + 20x_1 + 20x_2) $$

$$ \begin{array}{c|c|c} x_1 & x_2 & h_\Theta(x) \\
\hline 0 & 0 & 0 \\
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 1 \\
\end{array} $$

NOR

$$ \boldsymbol{ \Theta } = \begin{bmatrix} 10 & -20 & -20 \end{bmatrix} \\
\boldsymbol{ X } = \begin{bmatrix} 1 \\\ x_1 \\\ x_2 \end{bmatrix} \\
$$

$$ h_{ \Theta }(x) = g(\boldsymbol{ \Theta }\boldsymbol{ X }) = g(10 - 20x_1 - 20x_2) $$

$$ \begin{array}{c|c|c} x_1 & x_2 & h_\Theta(x) \\
\hline 0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0 \\
1 & 1 & 0 \\
\end{array} $$

XOR

レイア2に NAND と OR、レイア3に AND。

$$ \boldsymbol{ \Theta^{(1)} } = \begin{bmatrix} 30 & -20 & -20 \\ -10 & 20 & 20 \end{bmatrix} \\
\boldsymbol{ \Theta^{(2)} } = \begin{bmatrix} -30 & 20 & 20 \end{bmatrix} \\
\boldsymbol{ X } = \begin{bmatrix} 1 \\\ x_1 \\\ x_2 \end{bmatrix} \\
$$

$$ a^{(2)} = g(\boldsymbol{ \Theta^{(1)} }\boldsymbol{ X }) \\
a^{(3)} = g(\boldsymbol{ \Theta^{(2)} }\boldsymbol{ a^{(2)} }) \\
h_{ \Theta }(x) = a^{(3)} $$

$$ \begin{array}{c|c|c|c|c} x_1 & x_2 & a_{1}^{(2)} & a_{2}^{(2)} & h_\Theta(x) \\
\hline 0 & 0 & 1 & 0 & 0 \\
1 & 0 & 1 & 1 & 1 \\
0 & 1 & 1 & 1 & 1 \\
1 & 1 & 0 & 1 & 0 \\
\end{array} $$

XNOR

レイア2に AND と (NOT $x_1$) AND (NOT $x_2$)、レイア3に OR。

$$ \boldsymbol{ \Theta^{(1)} } = \begin{bmatrix} -30 & 20 & 20 \\ 10 & -20 & -20 \end{bmatrix} \\
\boldsymbol{ \Theta^{(2)} } = \begin{bmatrix} -10 & 20 & 20 \end{bmatrix} \\
\boldsymbol{ X } = \begin{bmatrix} 1 \\\ x_1 \\\ x_2 \end{bmatrix} \\
$$

$$ a^{(2)} = g(\boldsymbol{ \Theta^{(1)} }\boldsymbol{ X }) \\
a^{(3)} = g(\boldsymbol{ \Theta^{(2)} }\boldsymbol{ a^{(2)} }) \\
h_{ \Theta }(x) = a^{(3)} $$

$$ \begin{array}{c|c|c|c|c} x_1 & x_2 & a_{1}^{(2)} & a_{2}^{(2)} & h_\Theta(x) \\
\hline 0 & 0 & 0 & 1 & 1 \\
1 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 \\
1 & 1 & 1 & 0 & 1 \\
\end{array} $$

多クラス分類(Multiclass Classification)

多クラス分類(Multiclass Classification)の場合は、出力が下記のように複数持つようになり、該当要素だけを$1$にする。

$$ {h_\Theta(x) \approx \begin{pmatrix} 1\\
0\\
0\\
0 \end{pmatrix} , \hspace{10px} h_\Theta(x) \approx \begin{pmatrix} 0\\
1\\
0\\
0 \end{pmatrix} , \hspace{10px} h_\Theta(x) \approx \begin{pmatrix} 0\\
0\\
1\\
0 \end{pmatrix} , \hspace{10px} \hspace{10px} h_\Theta(x) \approx \begin{pmatrix} 0\\
0\\
0\\
1 \end{pmatrix} } $$