coursera 機械学習 7週目
Dec 1, 2017Large Margin Classification
Optimization objective
ロジスティック回帰のコスト関数は下記であった。
$$ min_\theta - \frac{1}{m} \sum_{i=1}^m \large[ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))\large] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2 $$
この目的関数を最小化するためには、$z=\theta^{T}x$として、下記の条件を満たす$\theta$を学習する必要があった。
- $y=1$のとき、$z \gg 0$
- $y=0$のとき、$z \ll 0$
サポートベクターマシン(support vector machine, SVM)のコスト関数では、
- $y=1$の時、$z \gt 1$は$0$
- $y=0$の時、$z \lt 1$は$0$
という前提条件をつける。
ロジスティック回帰のコスト関数との比較をグラフにすると下記のとおり。
$y=1$の時
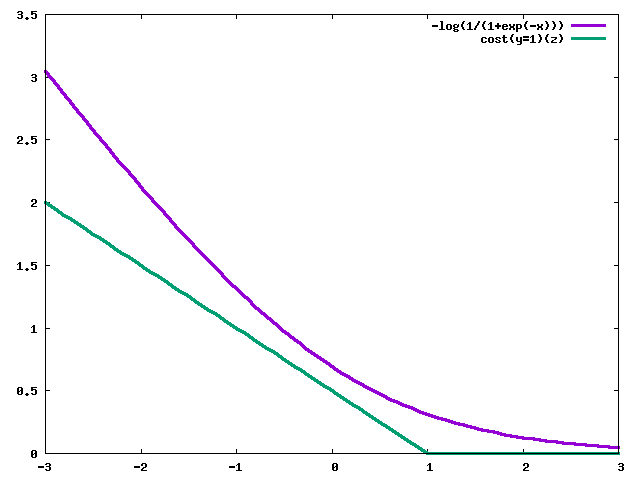
$y=0$の時
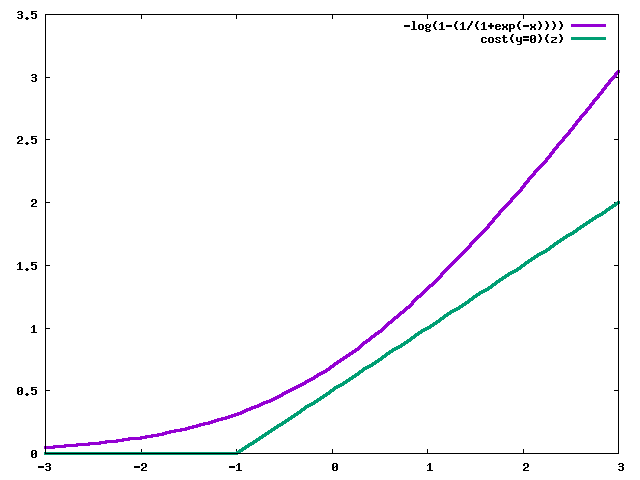
コスト関数は下記のようになる。
$$ min_\theta\ \frac{1}{m} \sum^m_{i=1} [y^{(i)} cost_1 (\theta^{\mathrm{T}} x^{(i)}) + (1 - y^{(i)}) cost_0 (\theta^{\mathrm{T}} x^{(i)})] + \frac{\lambda}{2m} \sum^n_{i=1} \theta^2_j $$
コスト関数は下記のようにも書ける。
$$ min_\theta\ C \sum^m_{i=1} [y^{(i)} cost_1 (\theta^{\mathrm{T}} x^{(i)}) + (1 - y^{(i)}) cost_0 (\theta^{\mathrm{T}} x^{(i)})] + \frac{1}{2} \sum^n_{i=1} \theta^2_j $$
$\lambda$は大きくなると正則化項の影響が大きくなり、小さくなると正則化項の影響を小さくなるので、$C=\frac{\lambda}{m}$となる変数を導入して、正則化項から$\lambda$を除去した下記のようなコスト関数でも意味的には同じになる。 $m$は第一項、第二項にあるので単純に除去。
このコスト関数は上記の前提条件
- $y=1$の時、$z \gt 1$は$0$
- $y=0$の時、$z \lt 1$は$0$
を踏まえて考えると
- $y^{(i)}=1$の時、$\theta^{T}x^{(i)} \geq 1$なら、$cost_1=0$
- $y^{(i)}=0$の時、$\theta^{T}x^{(i)} \leq -1$なら、$cost_0=0$
となり、この条件み満たすと第1項の$C$がついた項は$0$になるので、最小化問題で解くのは第2項のみでよくなる。
$$
min_\theta\ \frac{1}{2}\sum_{i=1}^{n}\theta_{j}^{2} \\
s.t. \hspace{15pt} \theta^{\mathrm{T}}x^{(i)} \ge 1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 1 \\
\hspace{30pt} \theta^{\mathrm{T}}x^{(i)} \le -1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 0
$$
Large Margin Intuition
決定境界(Decision Boundary)との距離をマージンという。
SVM(サポートベクターマシン)は、決定境界と各サンプルとの距離を最大化する$\theta$を選ぶことになる。
$C$の値が大きすぎると、1つの例外的なサンプルに合わせて、決定境界を過剰に変更しようとするが、$C$が適度な大きさであれば、最適な決定境界のままとなる。
Mathematics Behind Large Margin Classification
ベクトルの内積は下記のように表現される。
$$ \vec{x} \cdot \vec{y} = |x||y|\cos \theta $$
上記の意味的には、「ベクトル$\vec{x}$の長さ」と「ベクトル$\vec{y}$をベクトル$\vec{x}$に射影したもの長さ」の積である、ということである。
ベクトル$\vec{x}$とベクトル$\vec{y}$のなす角が$90^{\circ}$の場合は下記のようになる。
$$ \vec{x} \cdot \vec{y} = |x||y|\cos 90^{\circ} = |x||y| $$
SVM(サポートベクターマシン)の目的関数は$\theta$の数は2つだけだとすると下記のように表現できる。
$$ \frac{1}{2}\sum_{i=1}^{2}\theta_{j}^{2} = \frac{1}{2}(\theta_{1}^{2} + \theta_{2}^{2}) = \frac{1}{2}(\sqrt{\theta_{1}^{2} + \theta_{2}^{2}})^{2} = \frac{1}{2}||\theta||^{2} $$
つまり、ベクトル$\vec{\theta}$の長さの2乗を最小化することを意味する。
$$
min_\theta\ \frac{1}{2}\sum_{i=1}^{n}\theta_{j}^{2} = \frac{1}{2}||\theta||^{2} \\
s.t. \hspace{15pt} \theta^{\mathrm{T}}x^{(i)} \ge 1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 1 \\
\hspace{30pt} \theta^{\mathrm{T}}x^{(i)} \le -1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 0
$$
次に条件について理解を深めていく。
$$
\theta^{\mathrm{T}}x^{(i)} \ge 1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 1 \\
\theta^{\mathrm{T}}x^{(i)} \le -1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 0
$$
$\theta^{\mathrm{T}}x^{(i)}$はベクトル$\vec{\theta}$とベクトル$\vec{x^{(i)}}$の内積で、ベクトル$\vec{x^{(i)}}$をベクトル$\vec{\theta}$を射影した長さを$p^{(i)}$とすると下記のように書ける。
$$ \theta^{\mathrm{T}} x^{(i)} = p^{(i)}||\theta|| $$
つまり条件は下記のように書ける。
$$
p^{(i)}||\theta|| \ge 1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 1 \\
p^{(i)}||\theta|| \le -1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 0
$$
目的関数$\frac{1}{2}\sum_{i=1}^{n}\theta_{j}^{2}$を最小化するためには、$\theta$を大きくするわけにはいかず、$p^{(i)}$を大きくする必要がある。
投射の長さ$p^{i}$は決定境界(Decision Boundary)との距離で、つまりはマージン最大化することになる。
Kernels
KernelsⅠ
サポートベクターマシン(support vector machine, SVM)では、カーネル(Kernel)を使うことで非線形分類を行うことが可能になる。
カーネル(Kernel)を使うと、2つの点の類似度(similarity)を計算することができる。
比較を行うための点$l^{(i)}$をランドマーク(landmark)と呼ぶ。
今回はガウシアンカーネル(Gaussian Kernel)という手法を使う。
ガウシアンカーネル(Gaussian Kernel)は下記のように定義される。
$$ f_{i} = similarity(x,l^{(i)}) = exp(- \frac{||x - l^{(i)}||^2}{2\sigma^{2}}) $$
この関数は、$x$と$l^{i}$の距離が大きい場合$0$に近い値になり、距離が小さい場合は$1$に近い値になる。
$$
\begin{cases}
exp(- \frac{||x - l^{(i)}||^2}{2\sigma^{2}}) \approx 1 & (x \approx l^{(i)}) \\
exp(- \frac{||x - l^{(i)}||^2}{2\sigma^{2}}) \approx 0 & (x\ far\ from\ l^{(i)})
\end{cases}
$$
目的関数は、説明変数$x$をカーネル(Kernels)で計算した新たな説明変数$f_{i}$を使って下記のようになる。
$$ \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + … + + \theta_{i}x_{i} $$
KernelsⅡ
ランドマーク(landmark)$l^{i}$はトレーニングデータをそのまま使う。つまり、$l^{1}=x^{1}$, $l^{2}=x^{2}$,…,$l^{m}=x^{m}$となる。
サポートベクターマシン(support vector machine, SVM)とカーネル(Kernels)を組み合わせると、コスト関数は下記のように書ける。
$$
min_\theta\ C \sum^m_{i=1} [y^{(i)} cost_1 (\theta^{\mathrm{T}} f^{(i)}) + (1 - y^{(i)}) cost_0 (\theta^{\mathrm{T}} f^{(i)})] + \frac{1}{2} \sum^n_{i=1} \theta^2_j \\
s.t. \hspace{15pt} \theta^{\mathrm{T}}f^{(i)} \ge 1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 1 \\
\hspace{30pt} \theta^{\mathrm{T}}f^{(i)} \le -1 \hspace{10pt} if \hspace{5pt}y^{(i)} = 0
$$
各パラメータについての特徴。
パラメータ$C$は下記のような特徴がある。
- $C(=\frac{1}{\lambda})$が大きい時、偏り(bias)が小さくなり、分散(variance)が大きくなる。
- $C(=\frac{1}{\lambda})$が小さい時、偏り(bias)が大きくなり、分散(variance)が小さくなる。
パラメータ$\sigma^{2}$は下記のような特徴がある。
- $\sigma^{2}$が大きい時, 説明変数$f_{i}$はなめらかになる。つまり、偏り(bias)が大きくなり、分散(variance)が小さくなる。
- $\sigma^{2}$が小さき時, 説明変数$f_{i}$はなめらかではなくなる。つまり、偏り(bias)が小さくなり、分散(variance)が大きくなる。
SVMx in Practice
Using An SVM
線形カーネル(Linear Kernel, SVM withouot a Kernel)とガウシアンカーネル(Gaussian Kernel)がよく使われる。
それ以外のカーネルは下記のとおり。
- 多項式カーネル(Polynomial Kernel)
- 文字カーネル(String Kernel)
- カイの2乗カーネル(chi-square Kernel)
- ヒストグラムカーネル(histogram intersection Kernel)
どのアルゴリズムを使うべきか?
$n$を説明変数うの数、$m$をトレーニングセットの数だとすると
- $n$が大きい場合(n >=m, n=10000, m=1-1000)は、ロジスティック回帰、またはカーネルなしSVM(SVM without Kernel)
- $n$が小さく$m$が中間くらいの大きさの時(n=1-1000, m=10-10000)は、ガウシアンカーネルを使ったSVM(SVM with Gaussian Kernel)
- $n$が小さく$m$が大きい時(n=1-1000, m=50000+)は、より説明変数を加えた上で、ロジスティック回帰か、カーネルなしSVM(SVM without Kernel)
- ニューラルネットワークは上記のほとんどでうまくいく可能性があるが、トレーンニングが遅くなる可能性がある